leetcode

327. Count of Range Sum

题目

Given an integer array nums, return the number of range sums that lie in [lower, upper] inclusive.Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j (i ≤ j), inclusive.

**Note:**A naive algorithm of O(n2) is trivial. You MUST do better than that.

Example:

Input: nums = [-2,5,-1], lower = -2, upper = 2,
Output: 3 
Explanation: The three ranges are : [0,0], [2,2], [0,2] and their respective sums are: -2, -1, 2.

题目大意

给定一个整数数组 nums 。区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。请你以下标 i （0 <= i <= nums.length ）为起点，元素个数逐次递增，计算子数组内的元素和。当元素和落在范围 [lower, upper] （包含 lower 和 upper）之内时，记录子数组当前最末元素下标 j ，记作 有效 区间和 S(i, j) 。求数组中，值位于范围 [lower, upper] （包含 lower 和 upper）之内的 有效 区间和的个数。

注意： 最直观的算法复杂度是 O(n2) ，请在此基础上优化你的算法。

解题思路

• 给出一个数组，要求在这个数组中找出任意一段子区间的和，位于 [lower,upper] 之间。

• 这一题可以用暴力解法，2 层循环，遍历所有子区间，求和并判断是否位于 [lower,upper] 之间，时间复杂度 O(n^2)。

• 这一题当然还有更优的解法，用线段树或者树状数组，将时间复杂度降为 O(n log n)。题目中要求 lower ≤ sum(i,j) ≤ upper，sum(i,j) = prefixSum(j) - prefixSum(i-1)，那么 lower + prefixSum(i-1) ≤ prefixSum(j) ≤ upper + prefixSum(i-1)。所以利用前缀和将区间和转换成了前缀和在线段树中 query 的问题，只不过线段树中父节点中存的不是子节点的和，而应该是子节点出现的次数。第二个转换，由于前缀和会很大，所以需要离散化。例如 prefixSum = [-3,-2,-1,0]，用前缀和下标进行离散化，所以线段树中左右区间变成了 0-3 。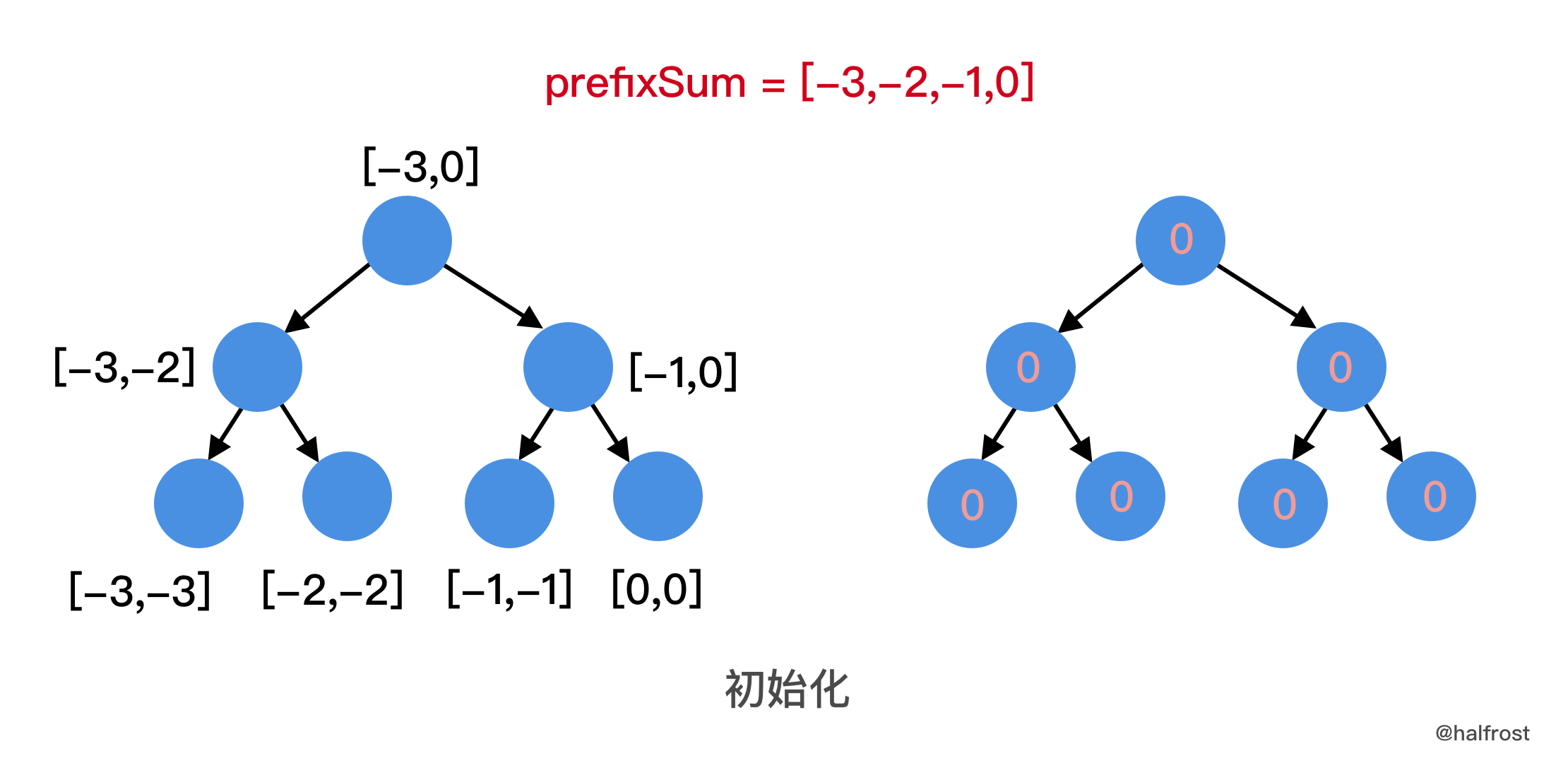

  

  利用 prefixSum 下标离散化：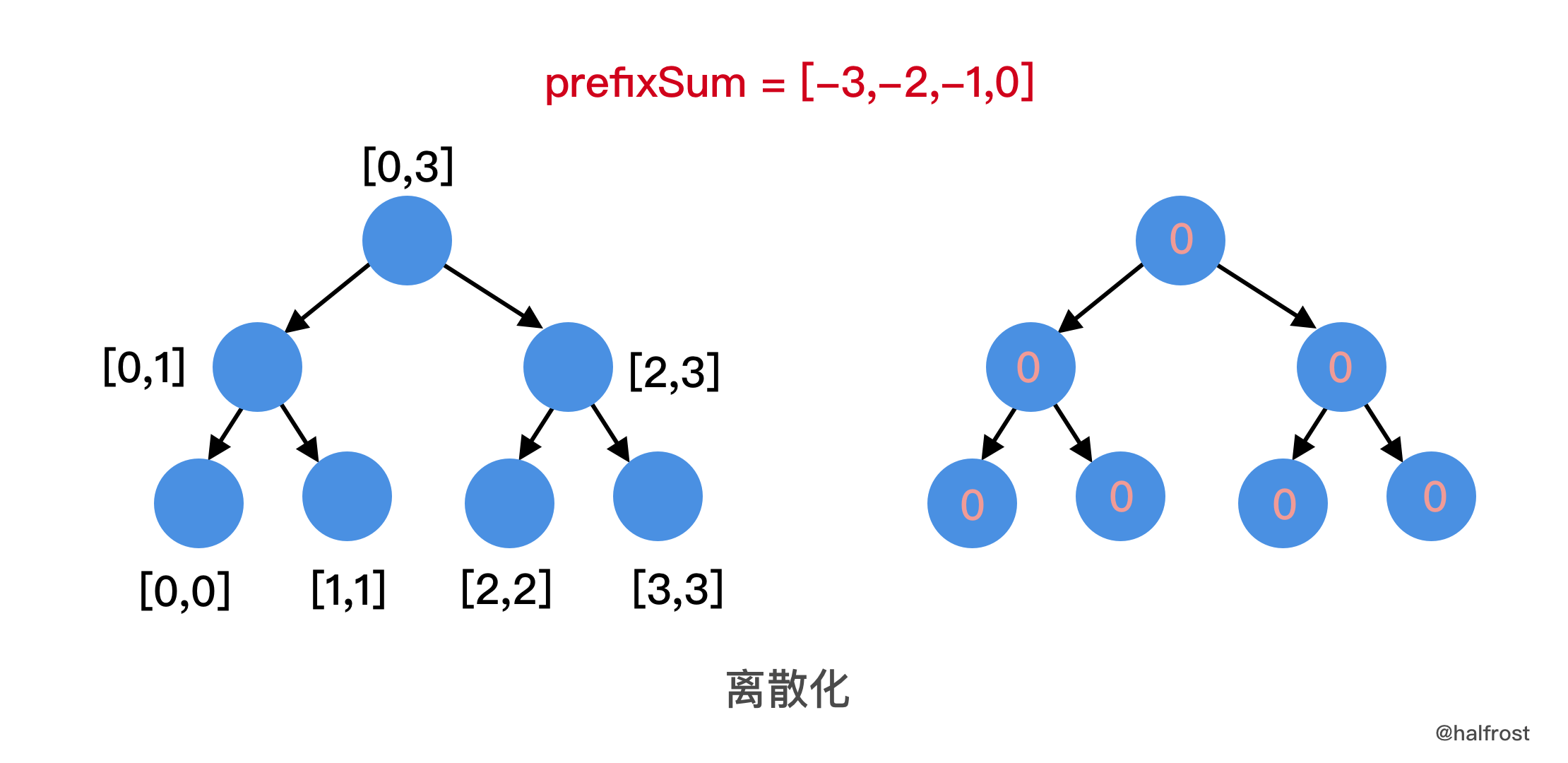

  

• 还需要注意一些小细节，prefixSum 计算完以后需要去重，去重以后并排序，方便构造线段树的有效区间。如果不去重，线段树中可能出现非法区间(left > right)或者重叠区间。最后一步往线段树中倒序插入 prefixSum 的时候，用的是非去重的，插入 prefixSum[j] 代表 sum(i,j) 中的 j，例如往线段树中插入 prefixSum[5]，代表当前树中加入了 j = 5 的情况。query 操作实质是在做区间匹配，例如当前 i 循环到 i = 3，累计往线段树中插入了 prefixSum[5]，prefixSum[4]，prefixSum[3]，那么 query 操作实质是在判断：lower ≤ sum(i=3,j=3) ≤ upper，lower ≤ sum(i=3,j=4) ≤ upper，lower ≤ sum(i=3,j=5) ≤ upper，这 3 个等式是否成立，有几个成立就返回几个，即是最终要求得的结果的一部分。

• 举个例子，nums = [-3,1,2,-2,2,-1]，prefixSum = [-3,-2,0,-2,0,-1]，去重以后并排序得到 sum = [-3,-2,-1,0]。离散化构造线段树，这里出于演示的方便，下图中就不画出离散后的线段树了，用非离散的线段树展示：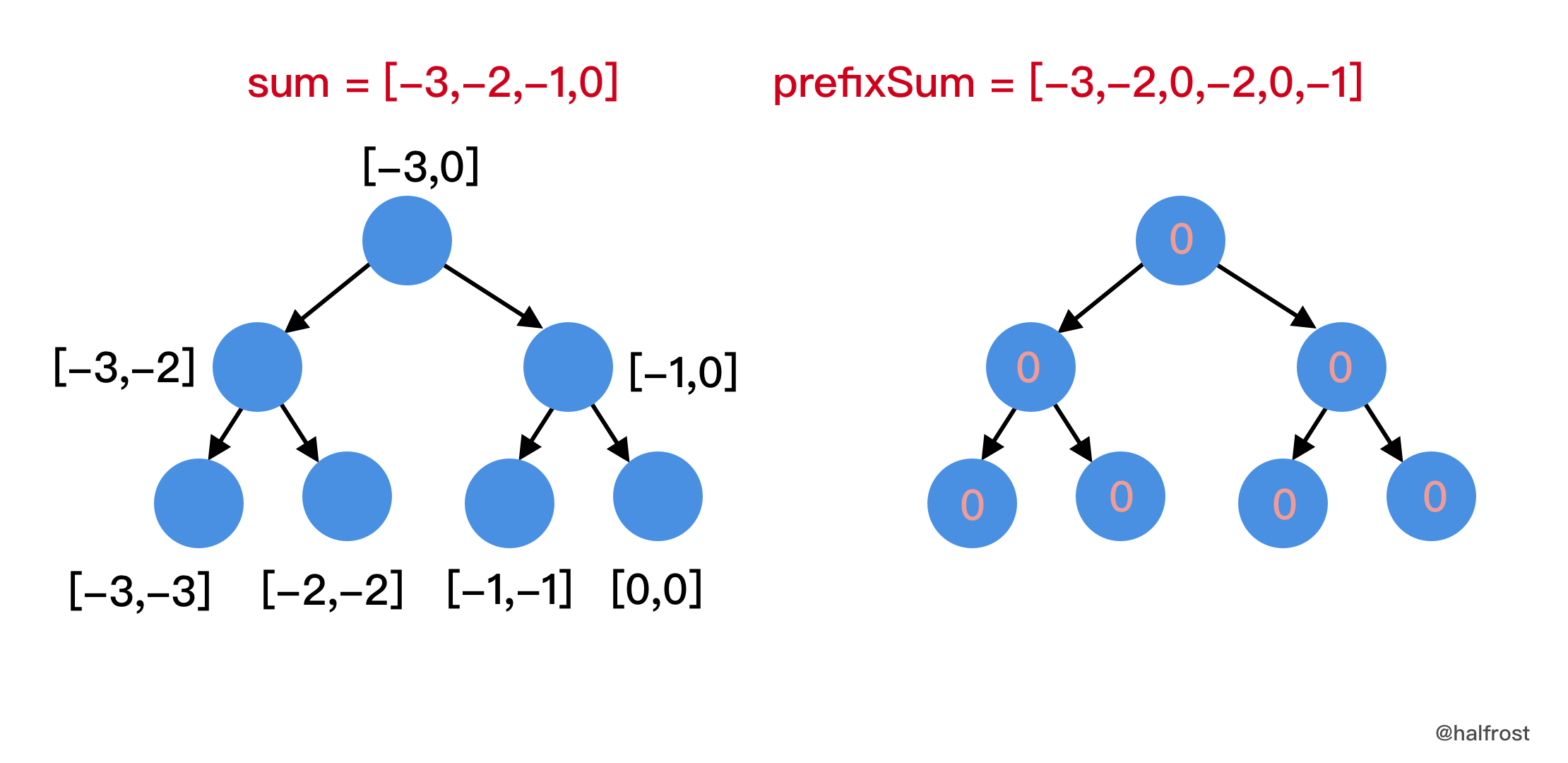

  

  倒序插入 len(prefixSum)-1 = prefixSum[5] = -1：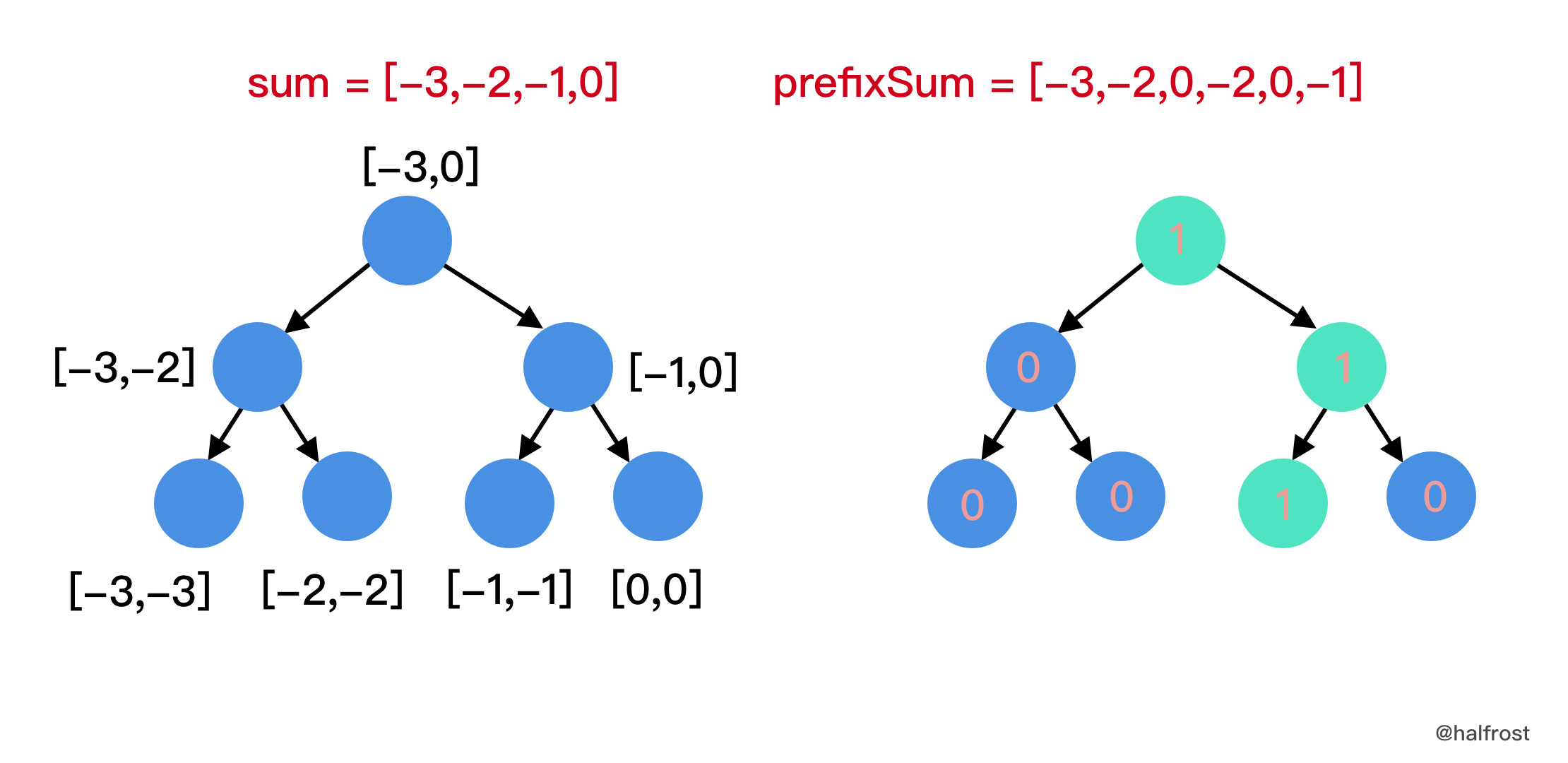

  

  这时候查找区间变为了 [-3 + prefixSum[5-1], -1 + prefixSum[5-1]] = [-3,-1]，即判断 -3 ≤ sum(5,5) ≤ -1，满足等式的有几种情况，这里明显只有一种情况，即 j = 5，也满足等式，所以这一步 res = 1。

• 倒序插入 len(prefixSum)-2 = prefixSum[4] = 0：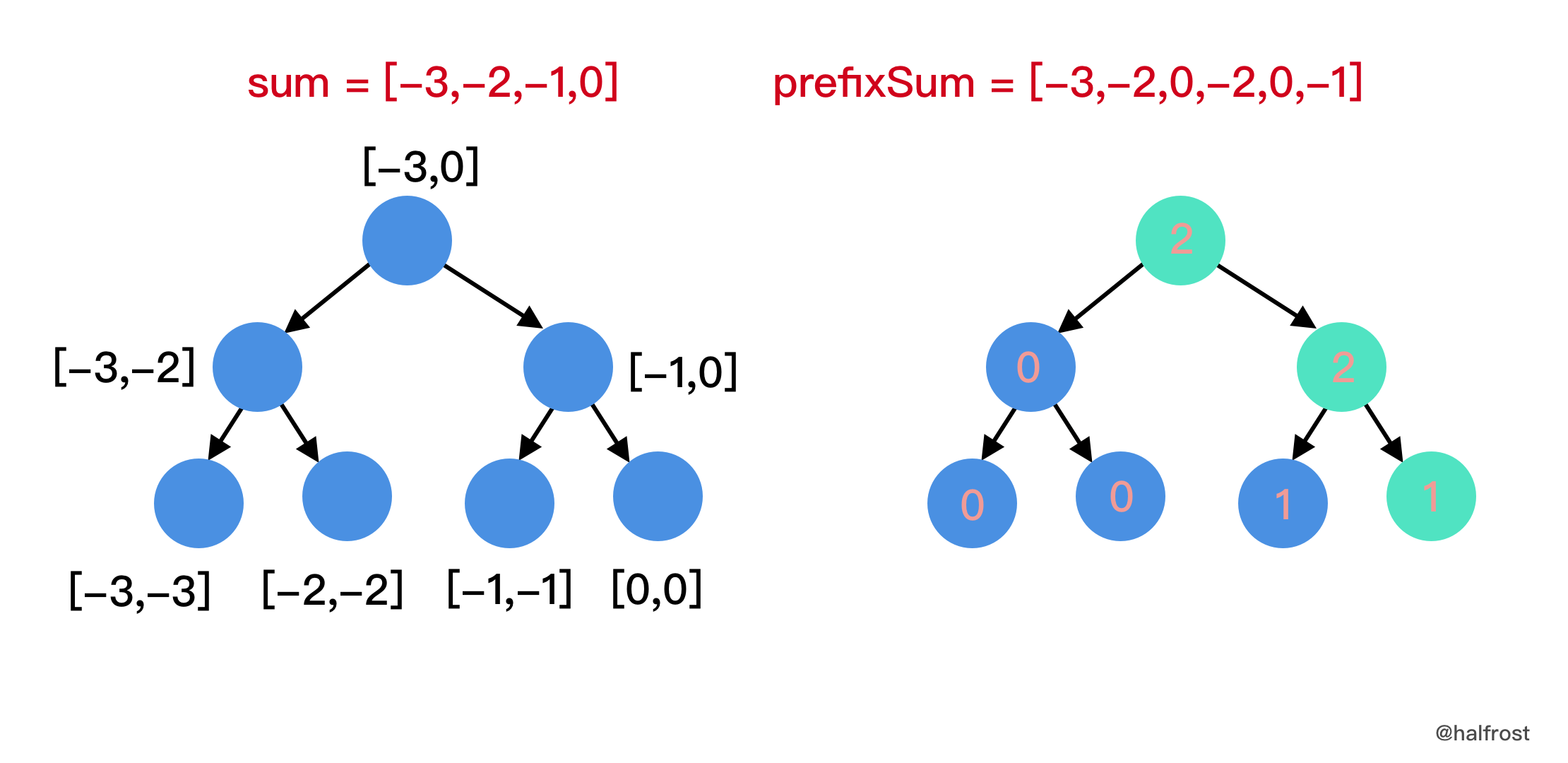

  

  这时候查找区间变为了 [-3 + prefixSum[4-1], -1 + prefixSum[4-1]] = [-5,-3]，即判断 -5 ≤ sum(4, 4,5) ≤ -3，满足等式的有几种情况，这里有两种情况，即 j = 4 或者 j = 5，都不满足等式，所以这一步 res = 0。

• 倒序插入 len(prefixSum)-3 = prefixSum[3] = -2：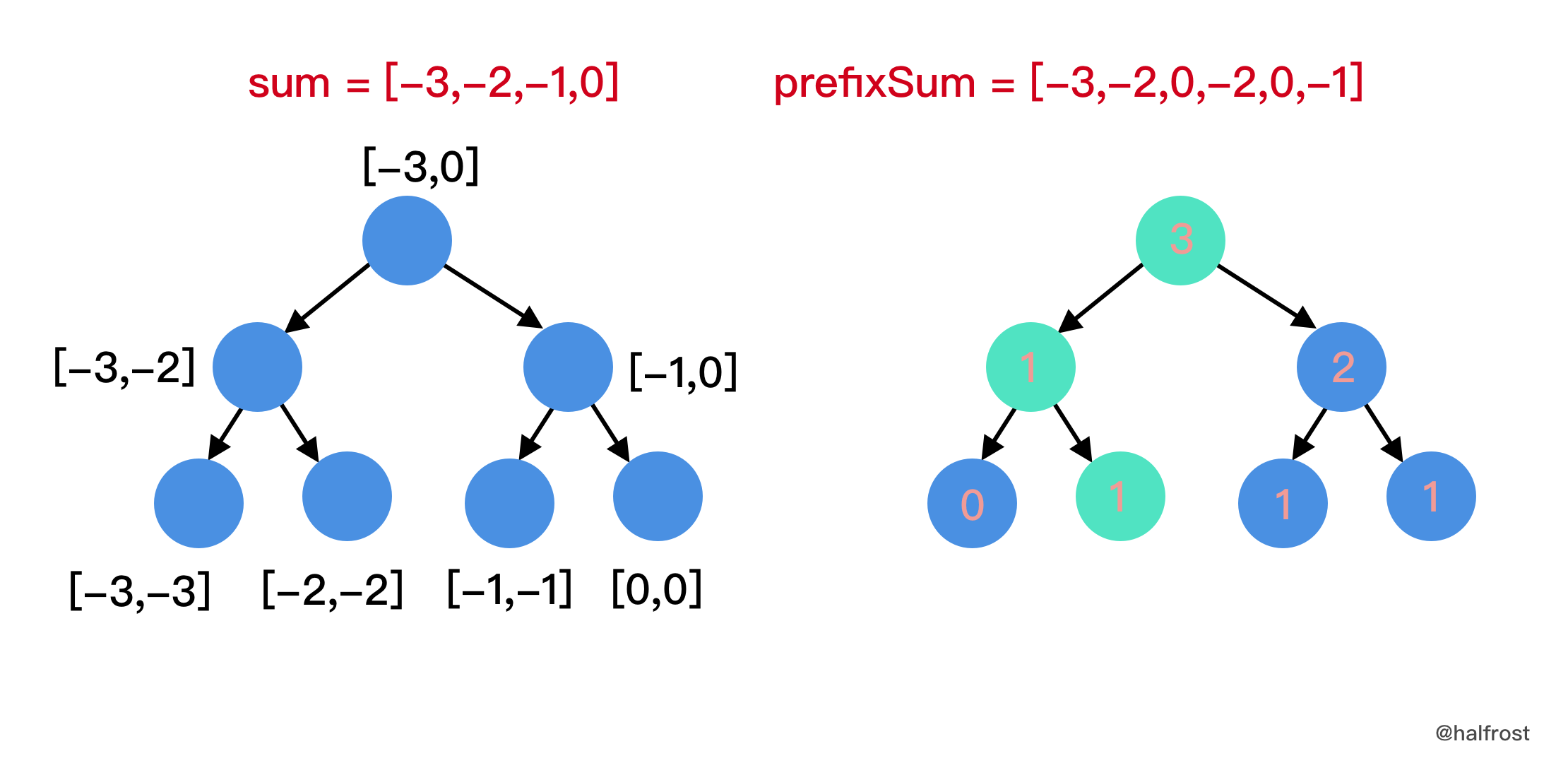

  

  这时候查找区间变为了 [-3 + prefixSum[3-1], -1 + prefixSum[3-1]] = [-3,-1]，即判断 -3 ≤ sum(3, 3,4,5) ≤ -1，满足等式的有几种情况，这里有三种情况，即 j = 3 、j = 4 或者 j = 5，满足等式的有 j = 3 和 j = 5，即 -3 ≤ sum(3, 3) ≤ -1 和 -3 ≤ sum(3, 5) ≤ -1。所以这一步 res = 2。

• 倒序插入 len(prefixSum)-4 = prefixSum[2] = 0：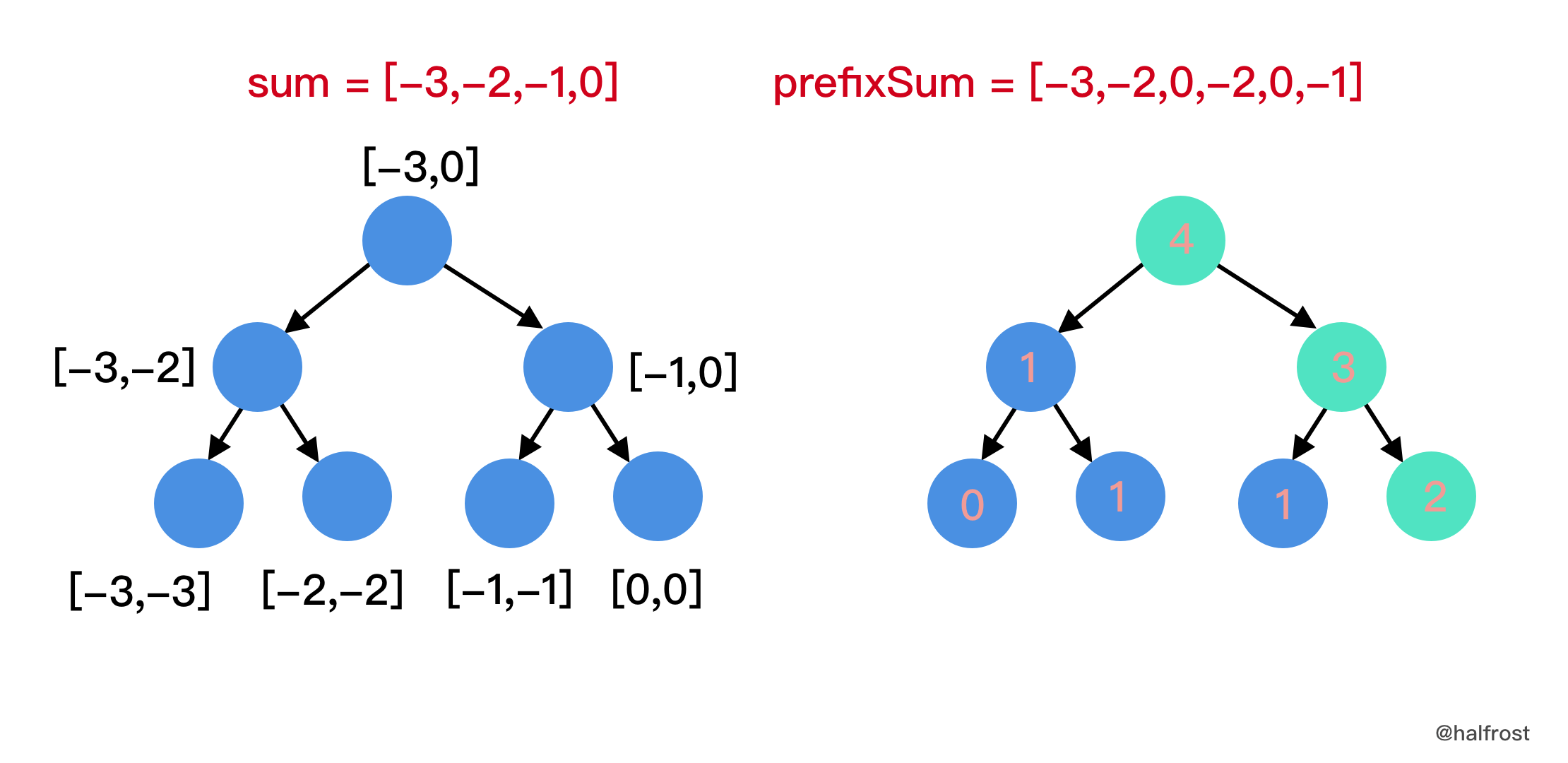

  

  这时候查找区间变为了 [-3 + prefixSum[2-1], -1 + prefixSum[2-1]] = [-5,-3]，即判断 -5 ≤ sum(2, 2,3,4,5) ≤ -3，满足等式的有几种情况，这里有四种情况，即 j = 2、 j = 3 、j = 4 或者 j = 5，都不满足等式。所以这一步 res = 0。

• 倒序插入 len(prefixSum)-5 = prefixSum[1] = -2：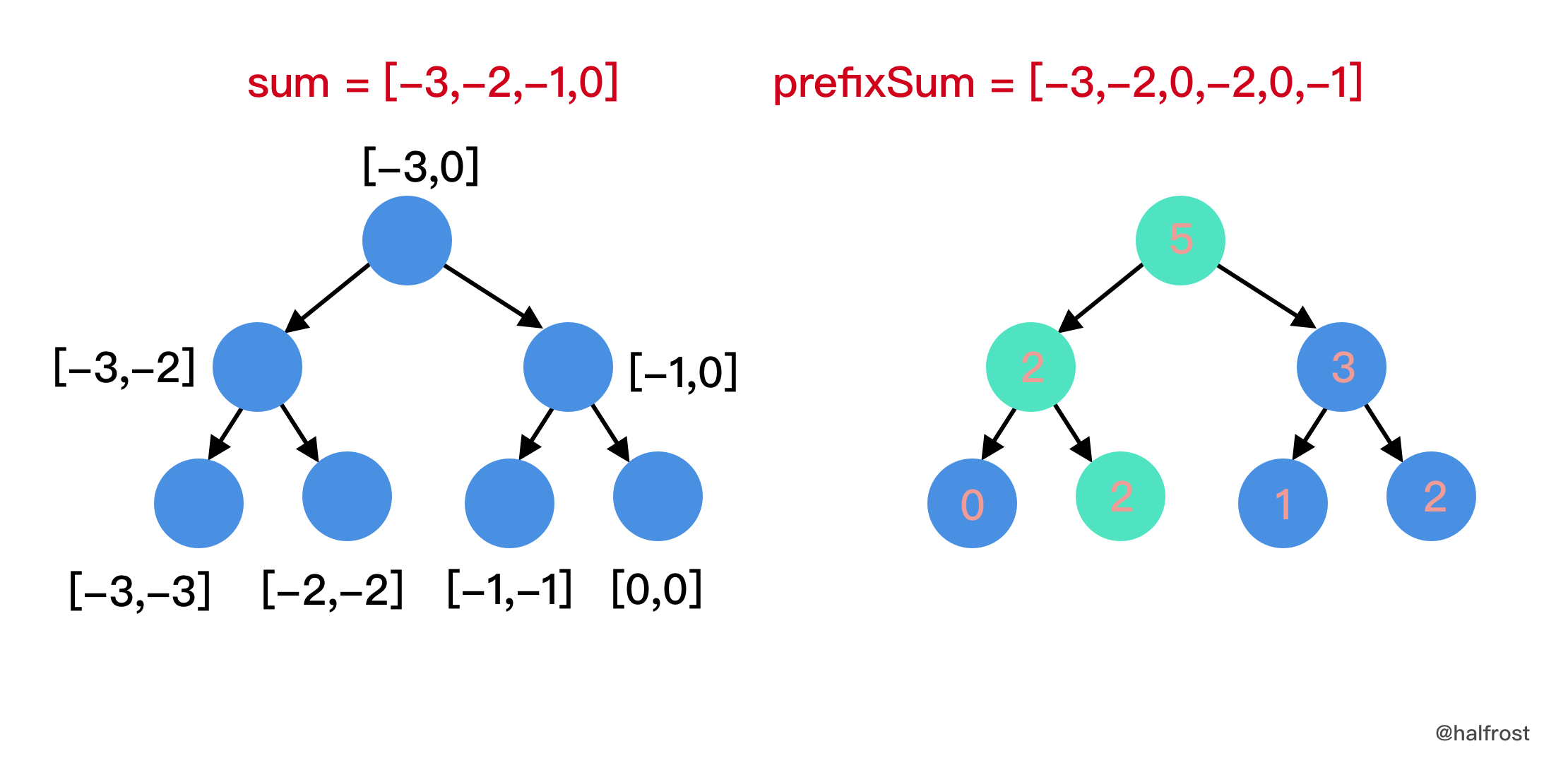

  

  这时候查找区间变为了 [-3 + prefixSum[1-1], -1 + prefixSum[1-1]] = [-6,-4]，即判断 -6 ≤ sum(1, 1,2,3,4,5) ≤ -4，满足等式的有几种情况，这里有五种情况，即 j = 1、 j = 2、 j = 3 、j = 4 或者 j = 5，都不满足等式。所以这一步 res = 0。

• 倒序插入 len(prefixSum)-6 = prefixSum[0] = -3：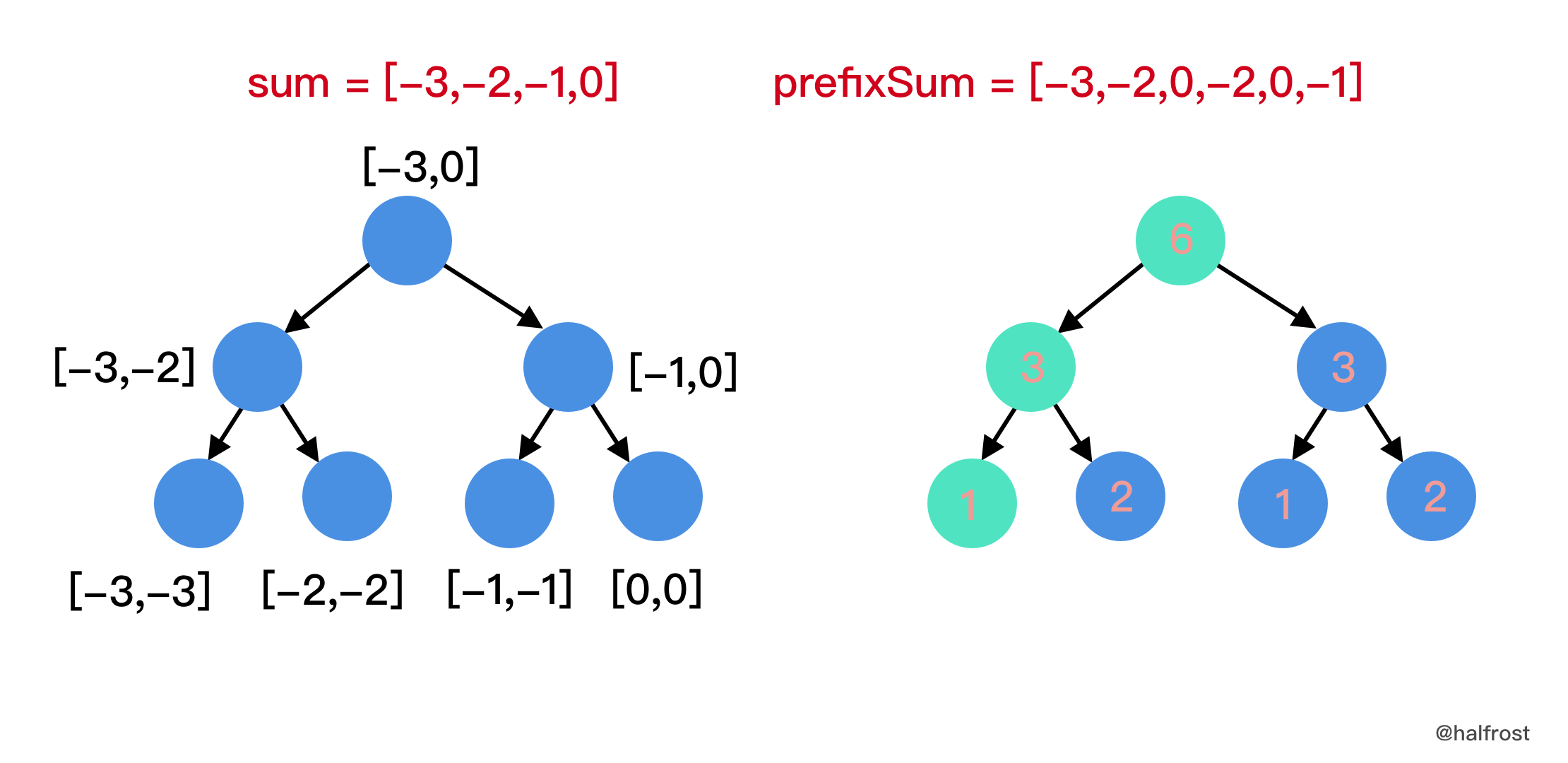

  

  这时候查找区间变为了 [-3 + prefixSum[0-1], -1 + prefixSum[0-1]] = [-3,-1]，注意 prefixSum[-1] = 0，即判断 -3 ≤ sum(0, 0,1,2,3,4,5) ≤ -1，满足等式的有几种情况，这里有六种情况，即 j = 0、j = 1、j = 2、 j = 3 、j = 4 或者 j = 5，满足等式的有 j = 0、j = 1、 j = 3 和 j = 5，即 -3 ≤ sum(0, 0) ≤ -1 、 -3 ≤ sum(0, 1) ≤ -1、-3 ≤ sum(0, 3) ≤ -1 和 -3 ≤ sum(0, 5) ≤ -1。所以这一步 res = 4。最后的答案就是把每一步的结果都累加，res = 1 + 0 + 2 + 0 + 0 + 4 = 7。

• 此题同样可以用树状数组来解答。同样把问题先转化成区间 Query 的模型，lower ≤ prefixSum(j) - prefixSum(i-1) ≤ upper 等价于 prefixSum(j) - upper ≤ prefixSum(i-1) ≤ prefixSum(j) - lower，i 的取值在 [0,j-1] 区间内。所以题目可以转化为 i 在 [0,j-1] 区间内取值，问数组 prefixSum[0...j-1] 中的所有取值，位于区间 [prefixSum(j) - upper, prefixSum(j) - lower] 内的次数。在树状数组中，区间内的前缀和可以转化为 2 个区间的前缀和相减，即 Query([i,j]) = Query(j) - Query(i-1)。所以这道题枚举数组 prefixSum[0...j-1] 中每个值是否出现在指定区间内出现次数即可。第一步先将所有的前缀和 prefixSum(j) 以及 [prefixSum(j) - upper, prefixSum(j) - lower] 计算出来。第二步排序和离散化，离散化以后的点区间为 [1,n]。最后根据数组 prefixSum(j) 的值在指定区间内查询出现次数即可。相同的套路题有，第 315 题，第 493 题。